[이득우 게임수학] 4. 삼각함수: 회전을 위한 수학

4.1 삼각함수

한 각이 직각(90도)인 직각삼각형을 이루는 세 변은 각 위치에 따라 빗변, 밑변, 높이 라고 부른다. 직각삼각형을 구성하는 세 변에서 두 변을 뽑아 각각의 비례관계를 나타낸 것은 삼각비(Trigonometric Ratio)라고 한다. 사인(Sine), 코사인(Cosine), 탄젠트(Tangent) 세가지가 대표적이다. 직각삼각형을 데카르트 좌표계 상에 배치하고 사잇각의 범위를 실수 전체로 확장한 대응 관계를 삼각함수(Trigonometric function)라고 한다.

삼각함수의 성질

sin 함수와 cos 함수의 그래프를 보면 [-1, 1] 범위내에서 360˚마다 반복되는데, 변화 값의 범위를 진폭(Amplitude), 반복되는 각도를 주기(Period)라고 한다. sin 함수와 cos함수의 성질을 정리하면 다음과 같다.

• sin 함수와 cos 함수는 항상 -1에서 1사이를 일정하게 반복하는 패턴을 띤다.
• sin 함수와 cos함수의 값은 360˚ 주기로 반복된다.
• cos함수는 y축을 기준으로 좌우 대칭의 성질을 가지고 있으며 짝함수(Even function)또는 우함수라고 부른다.
• sin함수는 원점을 기준으로 원점 대칭 성질을 가지고 있으며 홀함수(Odd function)또는 기함수라고 부른다.

tan 함수는 빗변과 무관하게 밑변과 높이의 관계만을 나타낸다.

각의 측정법

각(Angle)의 크기를 잴 때 0에서 360까지의 수를 사용하는 각도법(Degree)을 사용한다. 반원의 호 길이는 단위 벡터의 길이 1 보다 대략적으로 3.14배 더 크다. 이 값이 무리수인 원주율 파이(π)다. 180˚에 해당하는 반원의 호 길이가 파이임을 알았으니 반대로 호의 길이가 1인 부채꼴의 중심각은 몇도인가? 이 부채꼴의 각이 바로 호도법에서 사용하는 각의 기준인 1rad(라디안)이다. 1라디안은 약 52.2958˚로 무리수다.

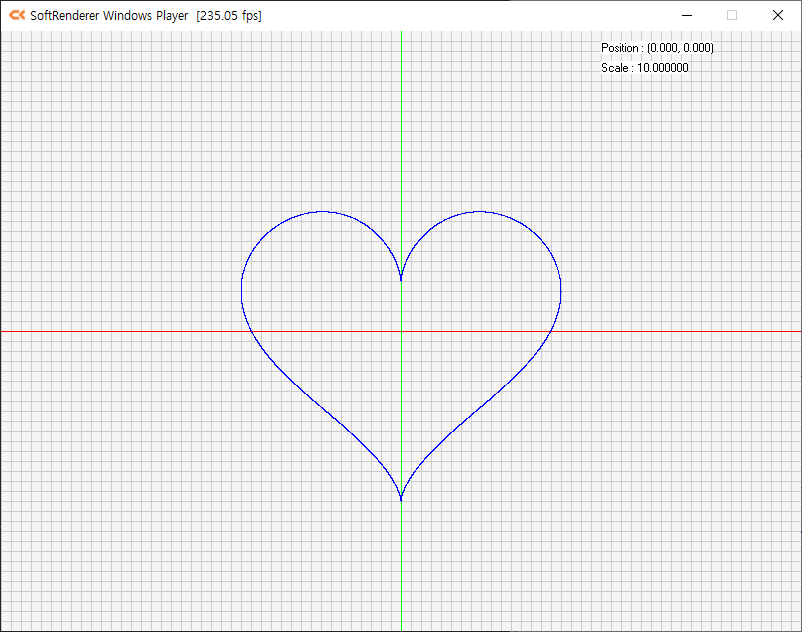
4-1 실습

삼각함수로 하트 그리기

4-2 실습

하트에 무지개 색상 입히기

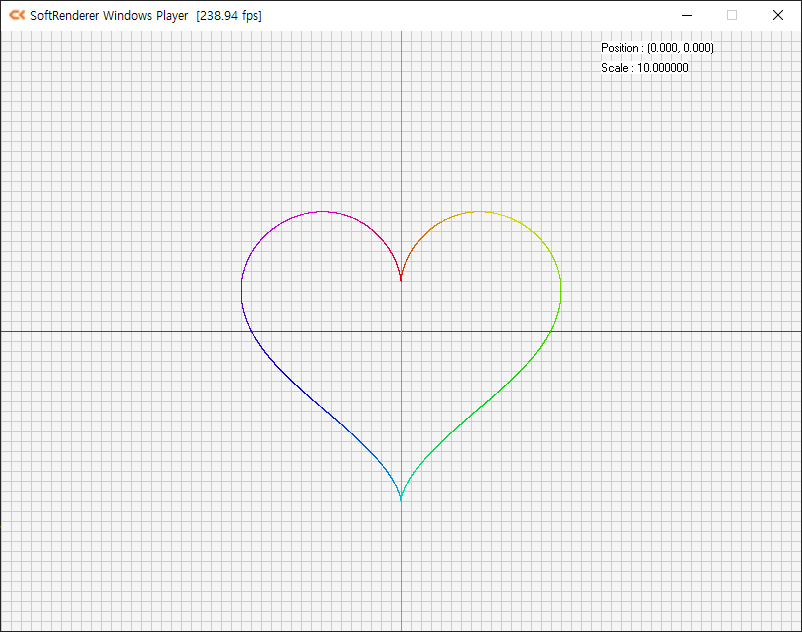
4-3 실습

두근대는 하트 애니메이션 만들기

4.2 삼각함수를 활용한 물체의 회전

기저벡터를 활용하여 회전한 좌표를 구해보자

e1 = (1, 0)
e2 = (0, 1)

이라고 할때 e1과 e2가 각 θ만큼 회전한 좌표를 e1', e2' 이라할 때

e1' = (cos θ, sin θ)
e2' = (-sin θ, cos θ)

임의의 벡터 u = (x,y)에 대해 각 θ만큼 회전한 벡터 u' = (x', y') 을 구할수 있는 수식을 정리한다면

u = (x, y) = x · e1 + y · e2 = x · (1,0) + y · (0,1)
u' = (x', y') = x · (cos θ, sin θ) + y · (-sin θ, cos θ)
   = (x cos θ - y cos θ, x sin θ + y cos θ)

   x' = x cos θ - y sin θ
   y' = x sin θ + y cos θ

4-4 실습

하트 회전시키기

4.3 삼각함수의 역함수

 f(x) = sin(x)
 f-1(x) = sin-1(x) = arcsin(x)

 cos-1(x) = arccos(x)
 tan-1(x) = arctan(x)

arctan 함수의 치역은 (-90˚, 90˚) 구간이므로 3사분면에 위치한 값을 넣으면 1사분면의 각정보가 나온다. 이럴때는 x,y 두값을 따로 전달하는 atan2 함수활용하면 모든 사분면에 대응하는 각도를 얻을 수 있다.

4.4 극좌표계

극좌표계(Polar coordinate system)은 회전 동작을 기반으로 설계된 좌표계이며 원점으로부터의 거리 r과 각도인 θ 두개의 요소로 구성되며 (r, θ) 로 표시한다.

r = sqrt(x^2, y^2)
θ = atan2(y,x)

x = r · cos θ
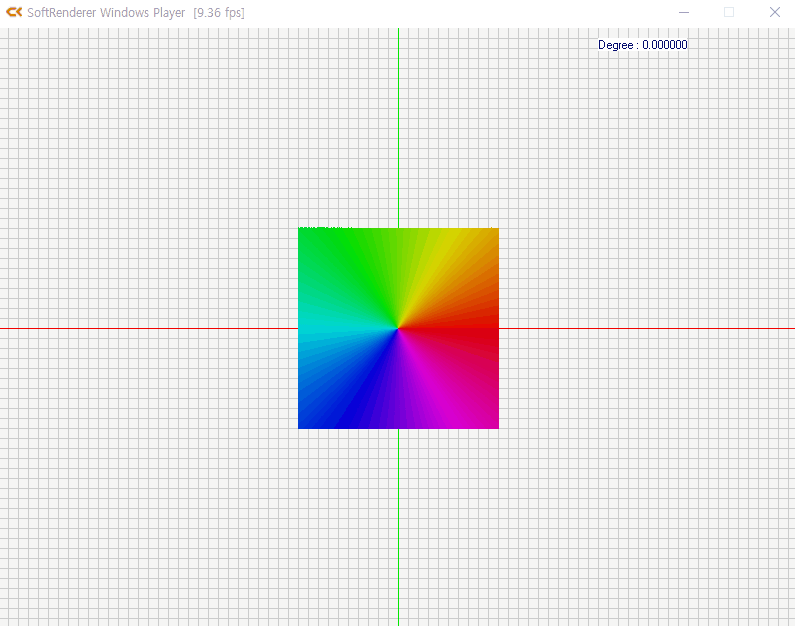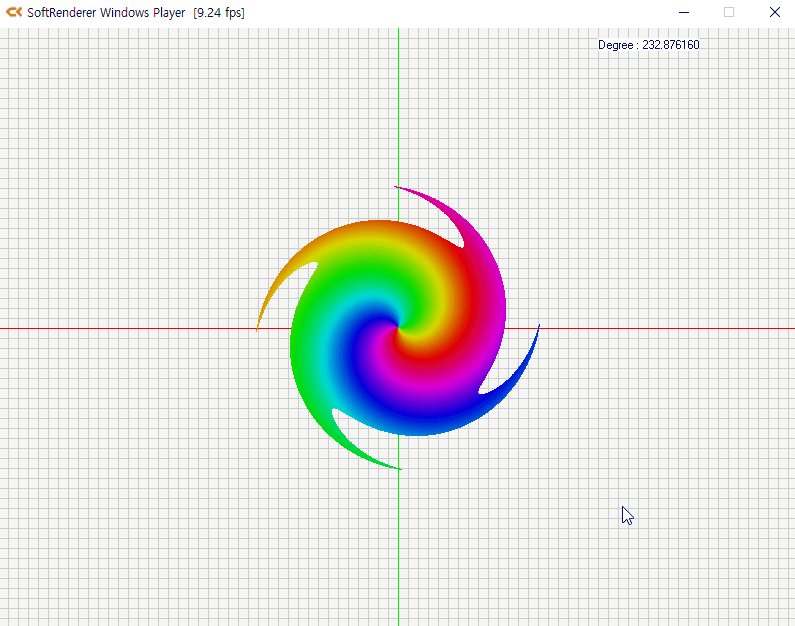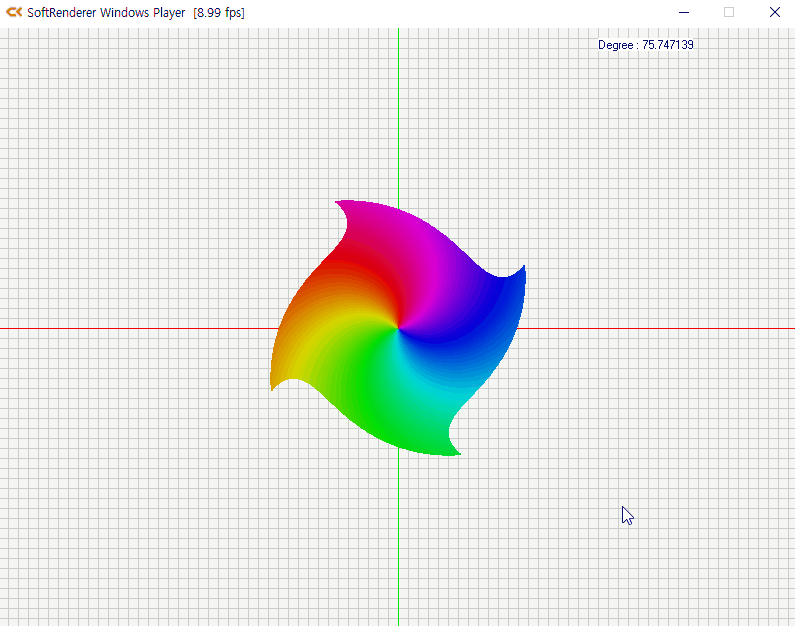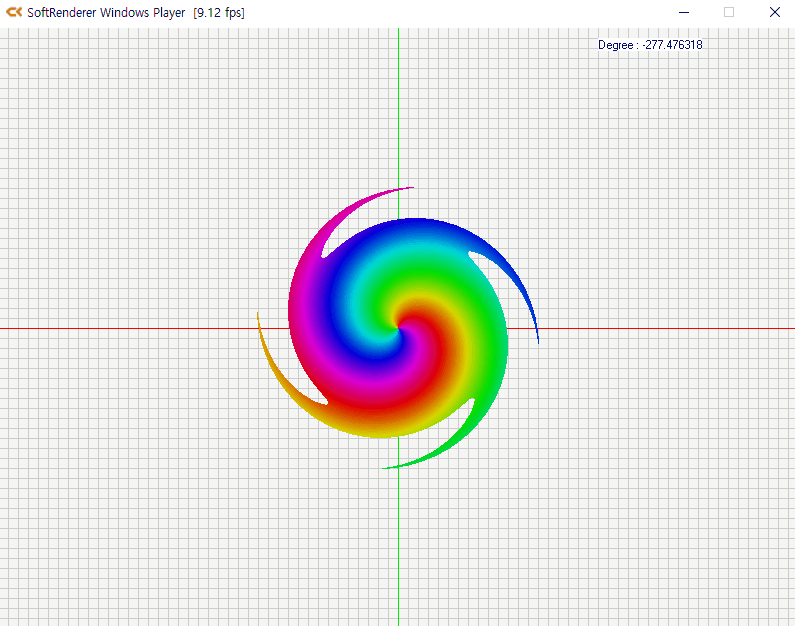
y = r · sin θ

4-5 실습

소용돌이 치는 특수 효과의 구현 원리

정리

• 삼각함수의 정의와 주요 성질
• atan2 함수에 대한 이해

출처

• 이득우의 게임수학 (https://www.onlybook.co.kr/entry/gamemath)