[이득우 게임수학] 7. 내적: 벡터 공간의 분석과 운용
- 📕 Book/이득우 게임수학
- 2023. 1. 25.
벡터 내적의 계산법과 내적이 가지는 성질을 알아보고 삼각함수와 어떤 연관성을 가지는지 알아보자
7.1 벡터의 내적
벡터의 내적(Dot product)은 같은 차원의 두 벡터가 주어졌을 때 벡터를 구성하는 각 성분을 곱한 후 이들을 더해 스칼라를 만들어내는 연산이다.
u = (a,b)
v = (c,d)
u·v = a·c + b·d내적의 성질
내적은 스칼라의 곱셈과 덧셈으로 구성되어 있으므로 교환법칙이 성립한다. 하지만 결과가 벡터가 아닌 스칼라로 나오는 성질로 인해 결합법칙은 성립하지 않는다.
u·v = a·c + b·d
v·u = c·a + d·b
∴ u·v = v·u
u·(v·w) ≠ (u·v)·w내적은 덧셈에 대한 분배법칙이 성립된다.
w·(u+v) = (e,f)·(a+c, b+d) = ae + ce + bf + df
u·w + v·w = (a,b)·(e,f) + (c,d)·(e,f) = ae + bf + ce + df
∴ w·(u+v) = u·w + v·w같은 벡터를 내적하면 벡터의 크기를 제곱한 결과가 나온다.
(x,y)·(x,y) = x^2 + y^2
∴ v·v = |v|^2내적은 교환법칙과 분배법칙이 성립하기 때문에, 두 벡터 합의 내적은 두 벡터의 크기로 표현할 수 있다.
(u+v)·(u+v) = u·u + v·v + 2(u·v)
= |u|^2 + |v|^2 + 2(u·v)내적과 삼각함수와의 관계
두 벡터 u,v의 사잇각을 θ라고 할 때 내적과 cos 함수의 관계는 다음과 같다
u·v = |u||v|cosθ행렬의 곱셈을 내적으로 표현하기
┌ a b ┐┌ x ┐ = ┌ ax + by ┐
└ c d ┘└ y ┘ └ cx + dy ┘
┌ ax + by ┐ = ┌ (a,b)·(x,y) ┐
└ cx + dy ┘ └ (c,d)·(x,y) ┘직교 행렬(Orthogonal matrix)은 정방행렬을 구성하는 모든 행벡터와 열벡터의 크기가 1이고 벡터들이 서로 직교하는 행렬이다. 직교행렬의 정의에 의해 벡터 (a,b)와 (c,d)는 서로 직교하므로 두 벡터의 내적은 0이 나온다. 따라서 직교행렬과 그 전치행렬의 곱은 언제나 항등행렬을 보장한다.
회전 변환행렬은 각 행벡터와 열벡터의 크기가 1이고 서로 직교하므로 직교행렬이다. 여러 종류의 선형 변환중 물체의 형태가 그대로 유지되는 선형 변환을 강체 변환(Rigid Transformation)이라고 한다.
- 변화된 기저벡터의 크기는 모두 1이어야 한다.
- 모든 기저벡터는 서로 직교해야 한다.
- 행렬식 값이 1이어야 한다.
det(R) = cos^2θ + sin^2θ = 17.2 시야 판별
앞뒤 판별
벡터 내적의 부호만 가지고도 두 벡터가 같은 방향을 향하는지 아니면 서로 마주보는지 확인할 수 있다.
- 벡터 내적의 결과가 양수 : 두 벡터는 같은 방향을 향하고 있다.
- 벡터 내적의 결과가 음수 : 두 벡터는 다른 방향을 향하고 있다.
- 벡터 내적의 결과가 0 : 두 벡터는 서로 직교한다.
캐릭터의 시선을 f 캐릭터에서 목표물로 향하는 벡터를 v라고 할때 두 벡터의 내적 f·v 의 부호에 따라 캐릭터와 목표물 사이의 공간 구성을 파악할 수 있다.
- f·v 결과의 부호가 양수 : 캐릭터 앞에 목표물이 있다.
- f·v 결과의 부호가 음수 : 캐릭터 뒤에 목표물이 있다.
- f·v 결과가 0 : 캐릭터 바로 옆에 목표물이 있다.
시야 판별
시야각이 β이고 캐릭터의 시선 단위벡터를 f, 캐릭터에서 목표물로 향하는 단위벡터를 v라고 할 때
f · v >= cos β/2 : 목표물이 시야 범위 안에 있음
f · v < cos β/2 : 목표물이 시야 범위 밖에 있음
atan2 함수를 활용해도 구할 수 있지만 단위벡터를 통해 내적을 계산하는 방식이 더 효율적이다.
7-1 실습
내적을 활용한 목표물 감지
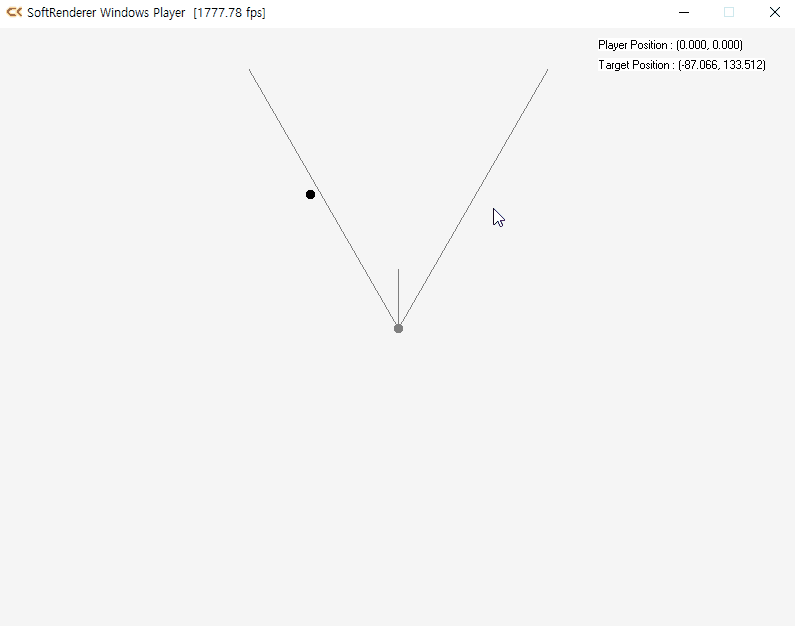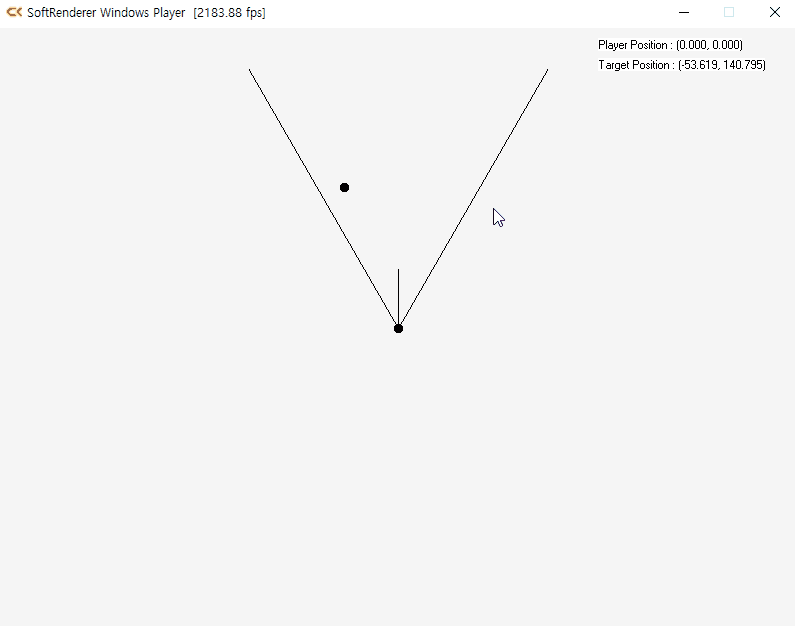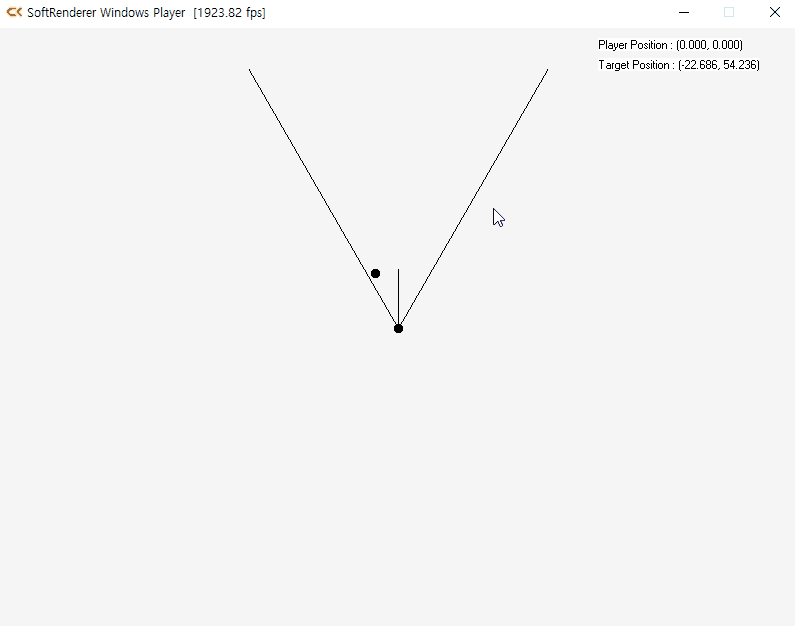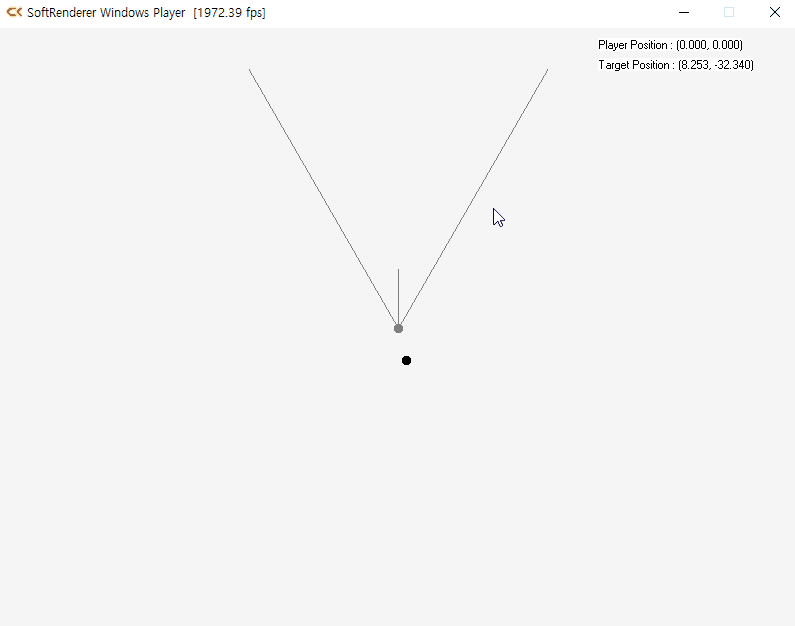
7.3 조명 효과의 구현
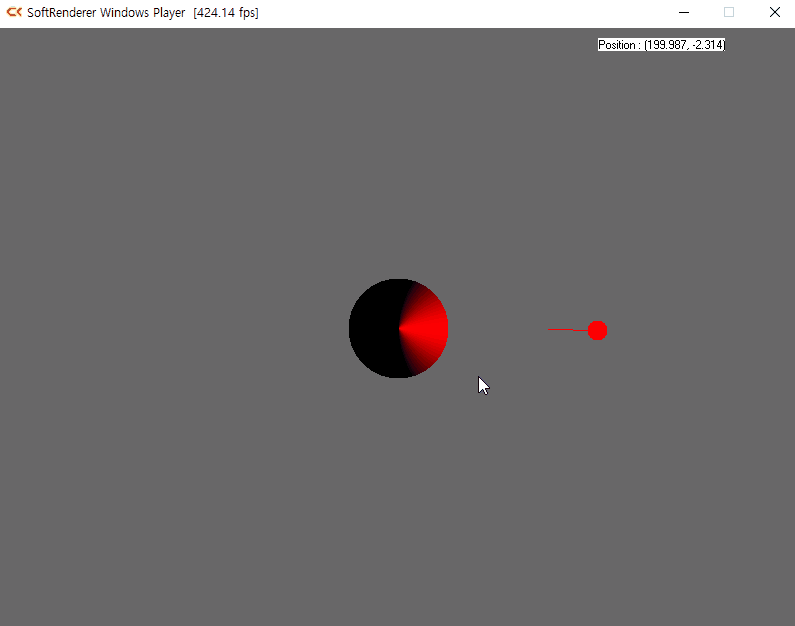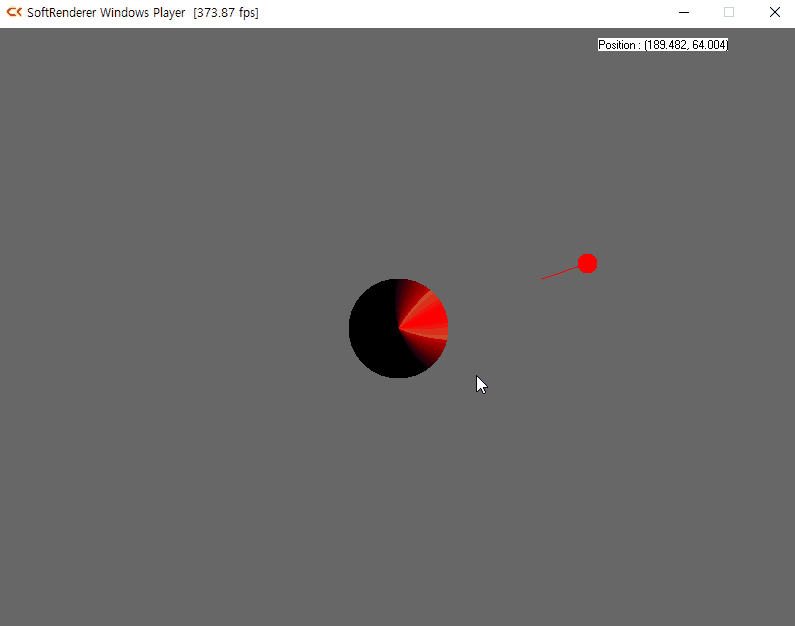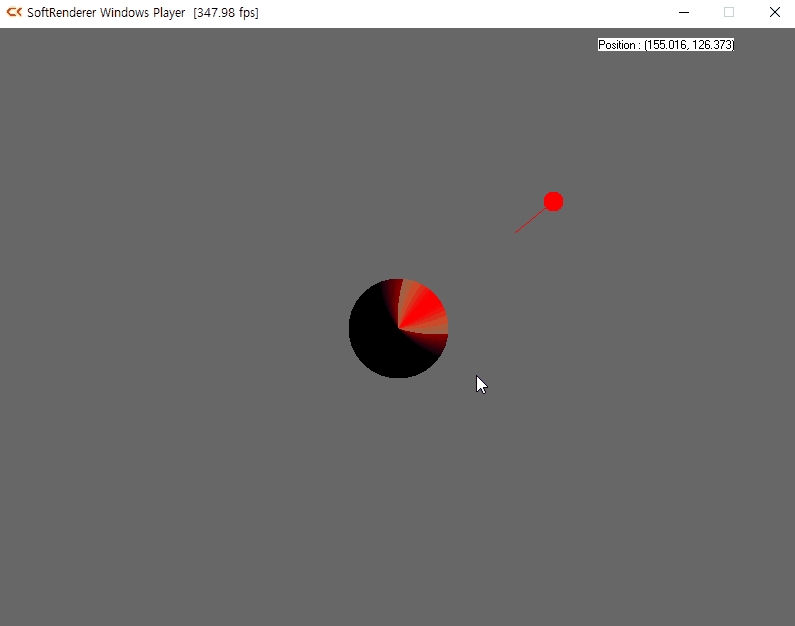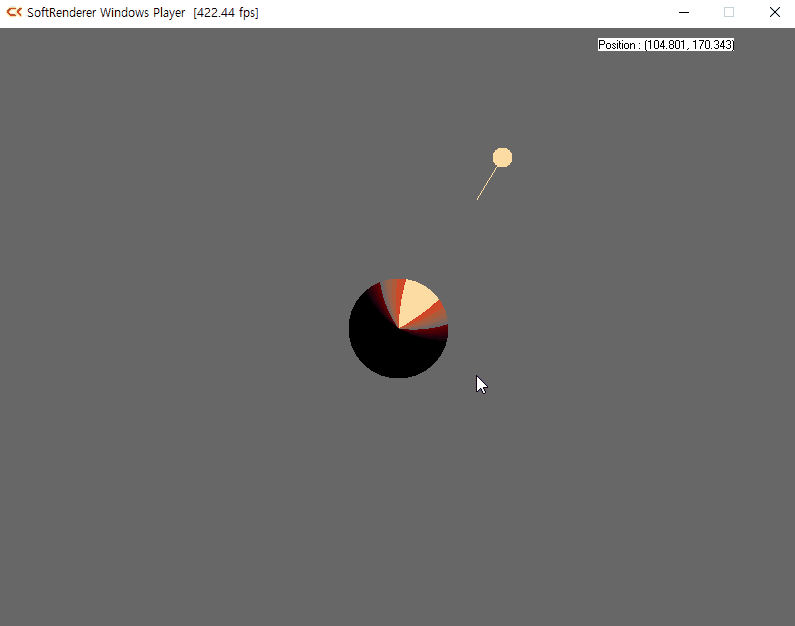
램버트 반사(Lambertian reflection)모델은 현실 세계와 비슷한 조명 효과를 만들기 위해 스위스의 수학자 요한 하인리히 램버트(Johann Heinrich Lambert)가 고안하였다. 빛을 받아 표면에서 반사되는 빛의 세기는 두 벡터가 만드는 사잇각의 cos 함수에 비례한다는 내용이다. 표면이 향하는 단위벡터를 N으로 지정하고 표면에서 광원으로 향하는 단위 벡터를 L로 지정한다면 두 벡터의 내적을 사용하여 사잇각 cos 값을 얻을 수 있다.
N · L = cosθ7-2 실습
내적을 활용한 조명 모델의 구현
7.4 투영 벡터
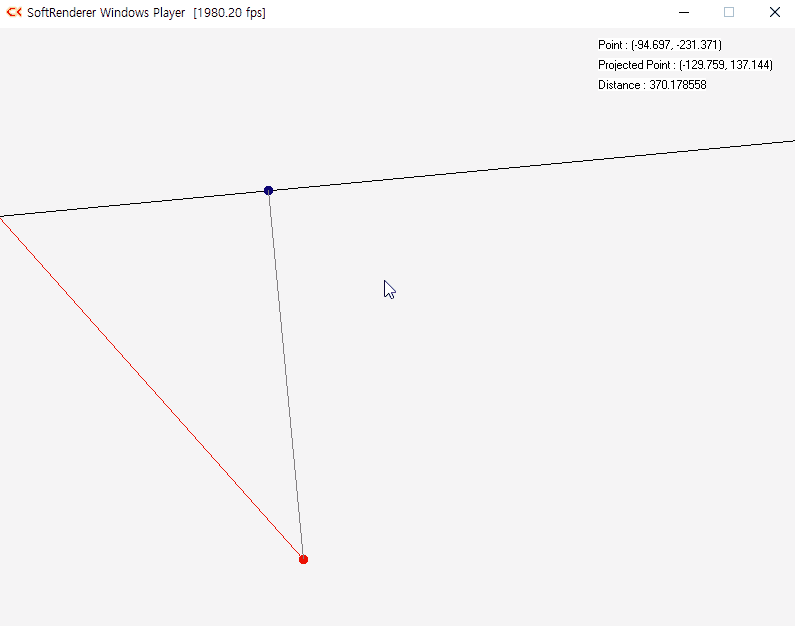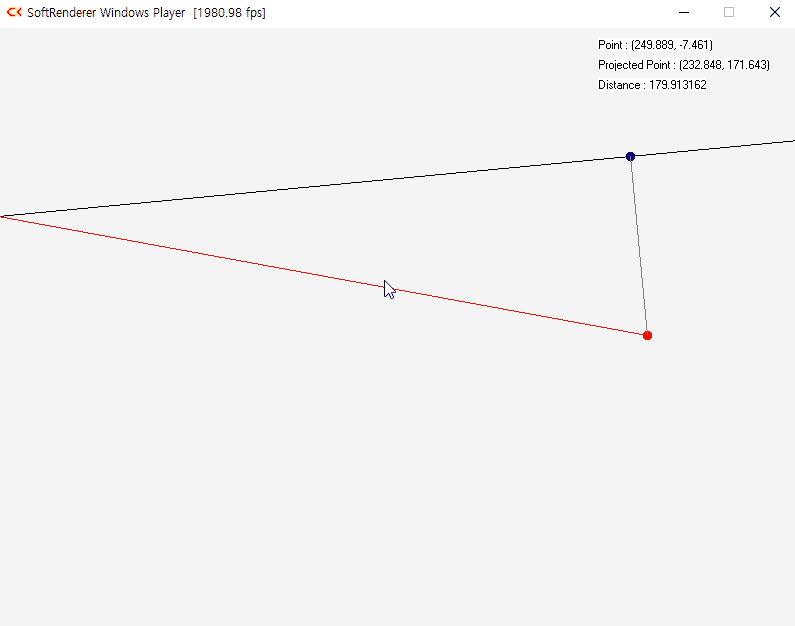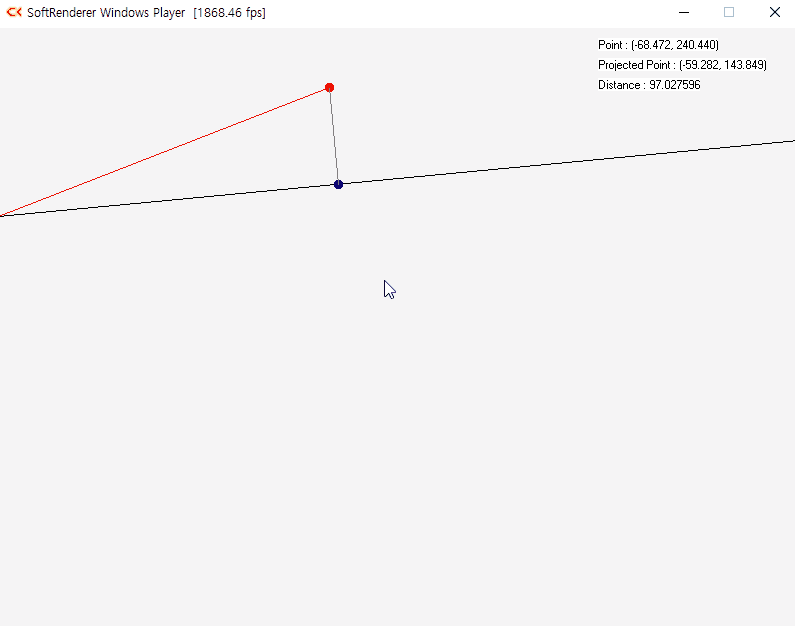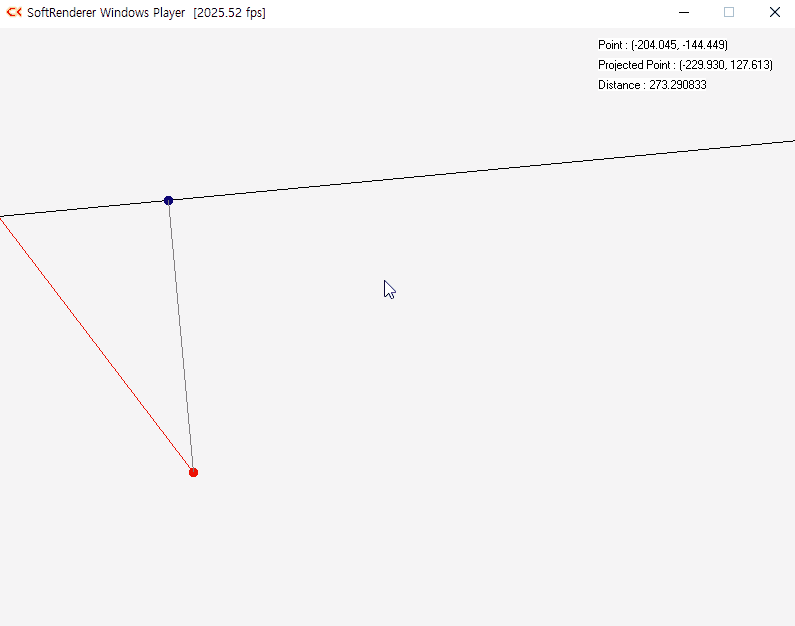
벡터 내적은 어떤 벡터를 다른 벡터에 직교 투영하는 용도로 사용된다. 벡터 v에 투영하려는 벡터 u가 있다고 할 때 v의 단위벡터를 구하고 투영하는 위치까지의 거리를 구하면 된다. 투영하는 거리는 |u|cosθ 로 구한다. cosθ는 u · v로 구할 수 있다.
//수식 생략
7-3 실습
내적을 활용한 벡터의 투영
7.5 정리
- 벡터의 내적에 대한 성질과 다양한 응용방법
- 투영 공식을 앞으로를 위해 익혀두자
출처
- 이득우의 게임수학 (https://www.onlybook.co.kr/entry/gamemath)